STL 关联式容器

STL关联式容器概述

特性

每个元素都有一个键值（key）和一个实值（value），以某种特定的规则将元素放到适合的位置，这一点和序列式容器vector,deque,list等不同，序列式容器中元素的位置和它们被插入的次序息息相关，关联式容器不在乎头尾，所以不会有push_back(),push_front(),pop_back(),pop_front(),begin(),end()等操作

关联式容器的内部结构一般是平衡二叉树（包括AVL-tree,RB-tree,AA-tree），其中RB-tree最为广泛

AVL-tree

导致不平衡（X的左右两颗子树的高度相差2）的四种情况：

• 1.插入点位于X的左子结点的左子树
• 2.插入点位于X的右子结点的右子树
• 3.插入点位于X的左子结点的右子树
• 4.插入点位于X的右子结点的左子树

对情况1,2的处理:单旋转

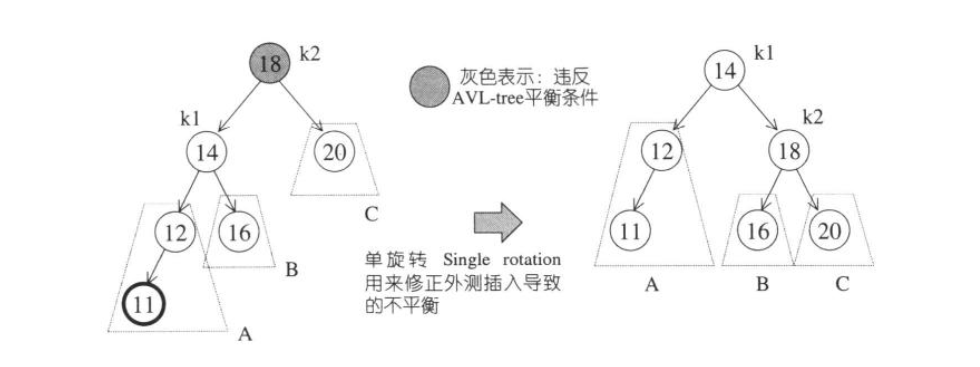
如图：一次顺时针的旋转

对情况3,4的处理:双旋转

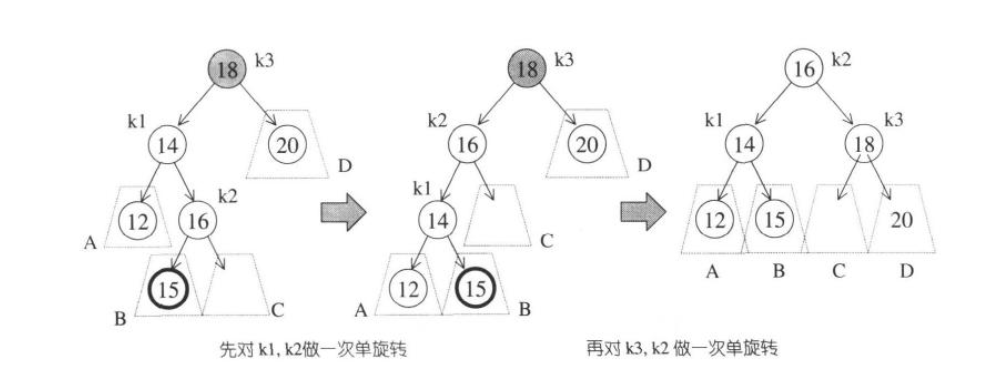
如图：一次逆时针的旋转，一次顺时针的旋转

RB-tree(红黑树)

红黑树的特征

• 每个节点不是红色就是黑色
• 根节点为黑色
• 如果节点为红，子节点必须是黑色
• 任意节点到末端的任何路径，所含黑节点数必须相同

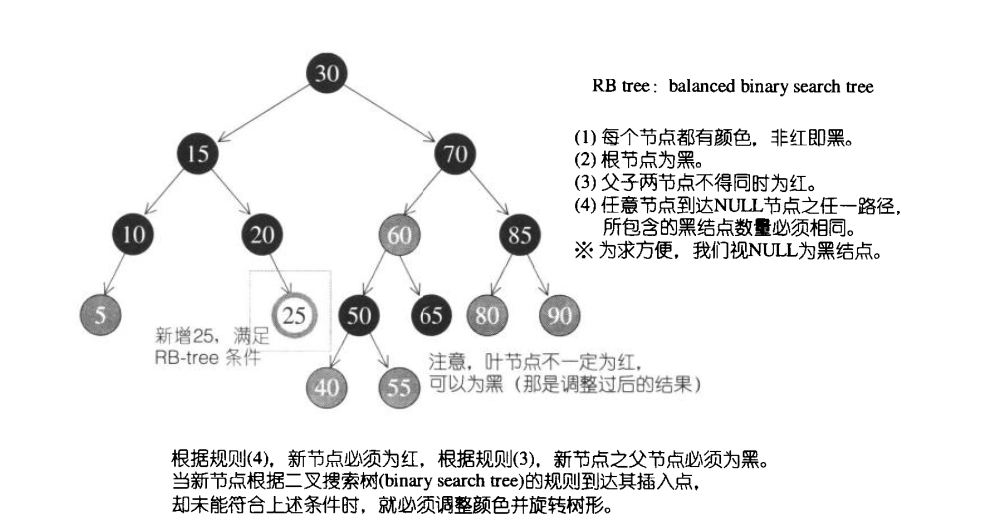
红黑树插入节点的四种情况

首先必须按照二叉搜索树的性质进行插入

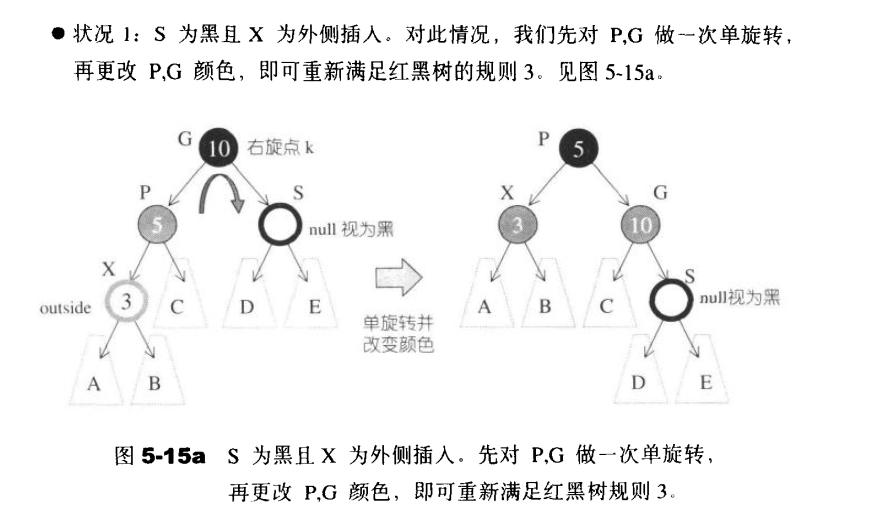
伯父节点为黑色的null且为外侧插入X：

单旋转之后，再把单旋转之后的X的兄弟和父亲节点进行变色

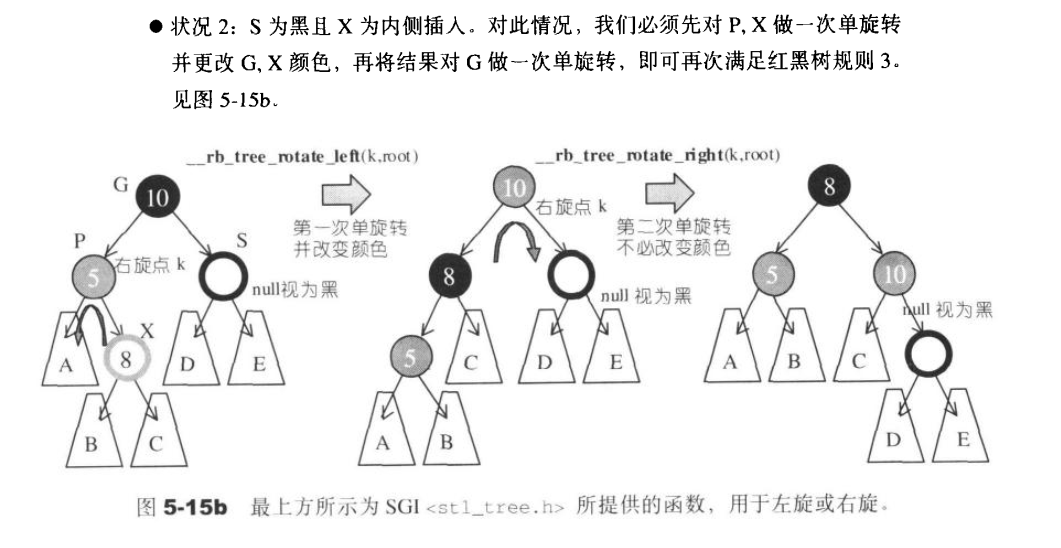
伯父节点为黑色的null且为内侧插入X：

双旋转之后，再把插入之前的爷爷节点进行变色

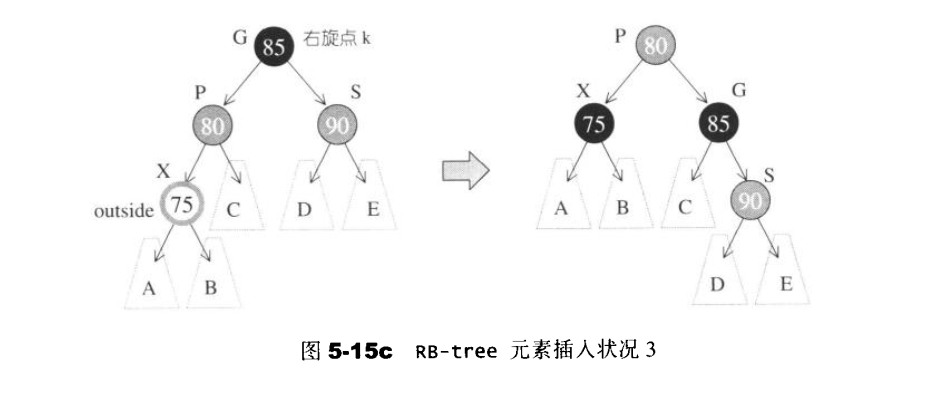
伯父节点为红色的且为外侧插入X，且爷爷的爸爸为黑色：

进行单旋转，不用变色

或者

把父亲，爷爷，伯父都变色

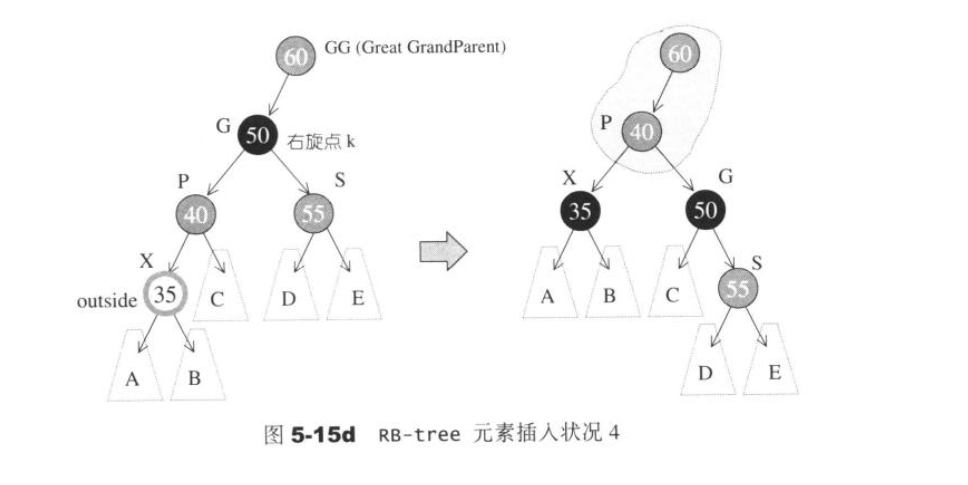
伯父节点为红色的且为外侧插入X，且爷爷的爸爸为红色：

把父亲，爷爷，伯父都变色，如果影响到了根节点，那么根节点不变色，依然为黑色

也可像下图一样旋转

向上递归

set的原理

set的元素不像map那样可以同时拥有实值和键值，set不允许两个元素有相同的键值

set不支持随机访问（只能用迭代器来访问第n小的元素），同时不可以通过set的迭代器来改变set的元素值，否则会严重改变set中红黑树的组织。

红黑树的结构保证了在插入或删除元素后，除非是被删除的元素本身，其他元素的迭代器都是稳定的，不会失效。这对需要频繁操作集合并保持对集合元素的引用是非常重要的。（回忆：vector则不同）

面对关联式容器使用STL算法find()来搜寻元素，可以有效运作，但不是好办法，因为STL的find()只是循序搜寻，而容器内部的find()是优化过的

auto it=find(iset.begin(),iset.end(),3);//尽量避免
auto it=iset.find(3);//正确

为什么用红黑树而不用AVL树？

就插入节点导致树失衡的情况，AVL和RB-Tree都是最多两次树旋转来实现复衡rebalance，旋转的量级是O(1) 删除节点导致失衡，AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而RB-Tree最多只需要旋转3次实现复衡，只需O(1)，所以说RB-Tree删除节点的rebalance的效率更高，开销更小！

set的函数接口

insert操作：

insert返回值为std::pair<iterator,bool类型>，前者返回迭代器，后者返回插入成功与否

erase操作：

注意erase操作会将原有的迭代器失效

//这段代码存在问题
std::set<int> my_set = { 4,1,3,6,5 };
auto it = my_set.begin();
my_set.erase(it);
std::cout << *it << std::endl;

map

不可以通过map的迭代器来改变map的键值，但是可以改变元素的实值

map自定义比较函数：

auto compare = [](const int& num1, const int& num2) {return num1 > num2; };
std::map<int,int,decltype(compare)> my_map(compare);
my_map.insert({ 1,5 });
my_map.insert({ 6,5 });
my_map.insert({ 4,5 });
my_map.insert({ 2,5 });
for (auto elem : my_map)
{
	std::cout << elem.first << " " << elem.second << std::endl;
}