Dijkstra算法

参考：https://leetcode.cn/problems/network-delay-time/solutions/2659415/dijkstra-po-su-yu-dui-you-hua-dai-ma-sui-kp1q/

Dijkstra算法解释

基本思想

dijkstra三部曲：

• 第一步，选源点到哪个节点近且该节点未被访问过
• 第二步，该最近节点被标记访问过（访问过代表改点已经找到最短路径）
• 第三步，根据第二部得到的节点更新非访问节点到源点的距离（即更新minDist数组）

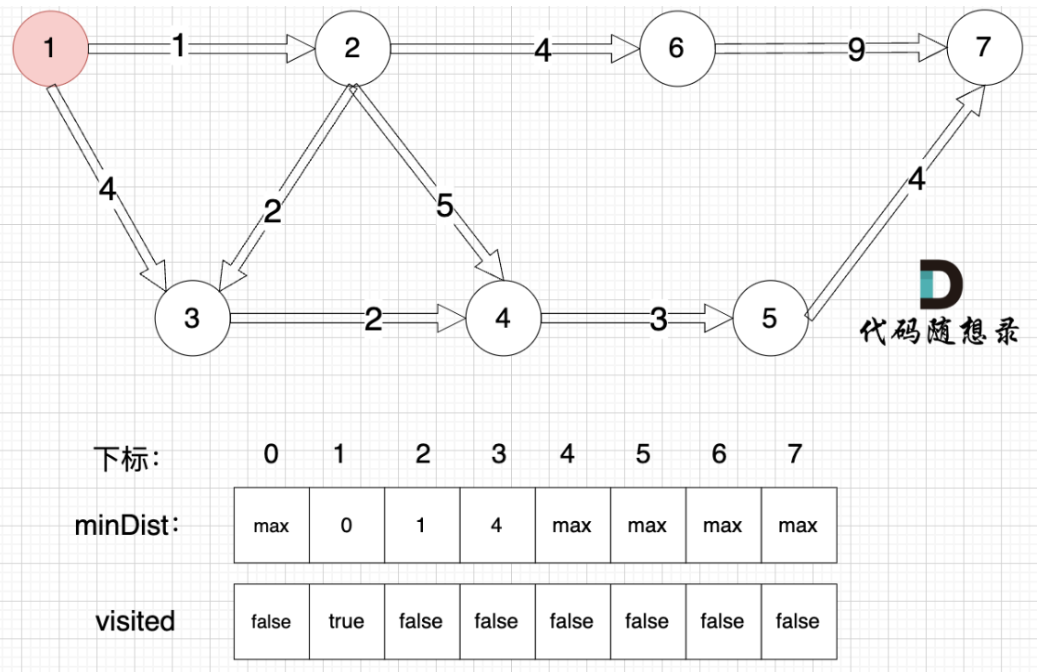
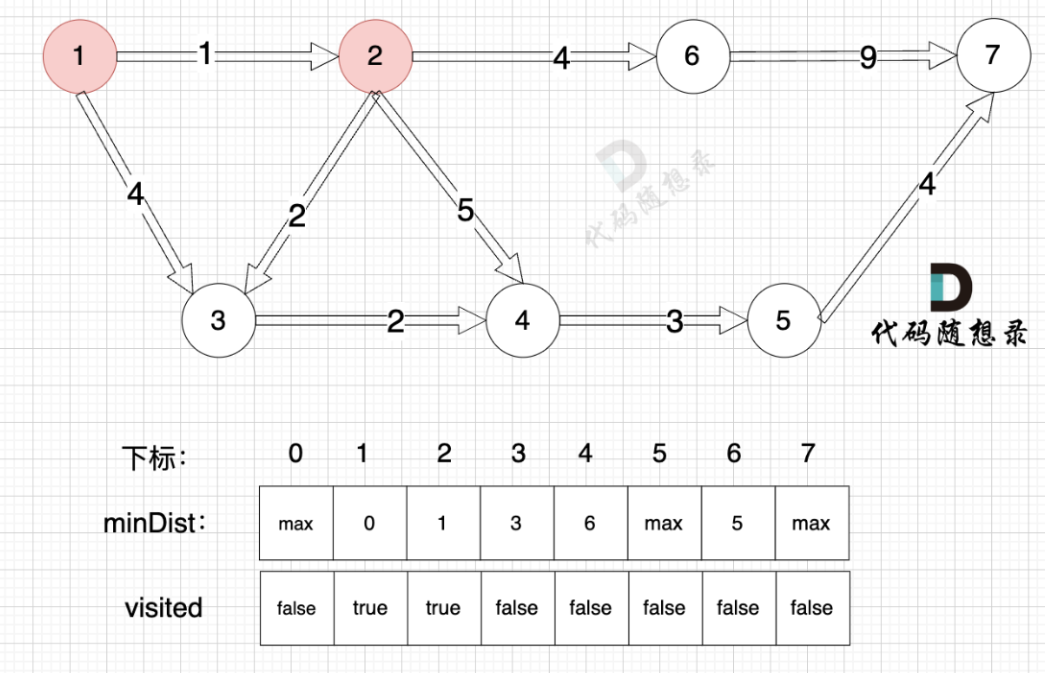
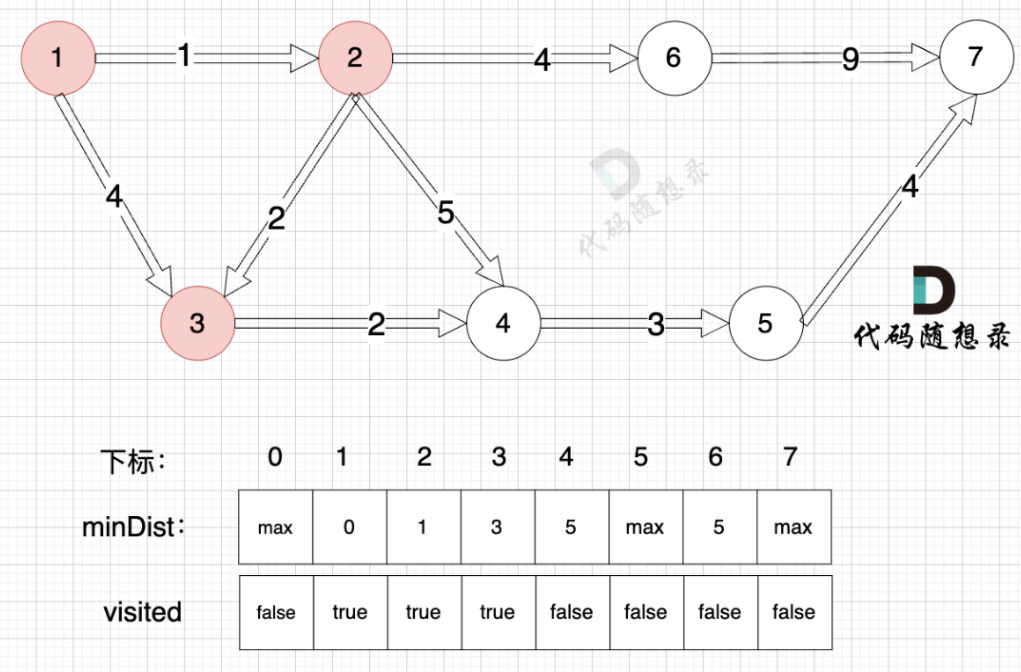
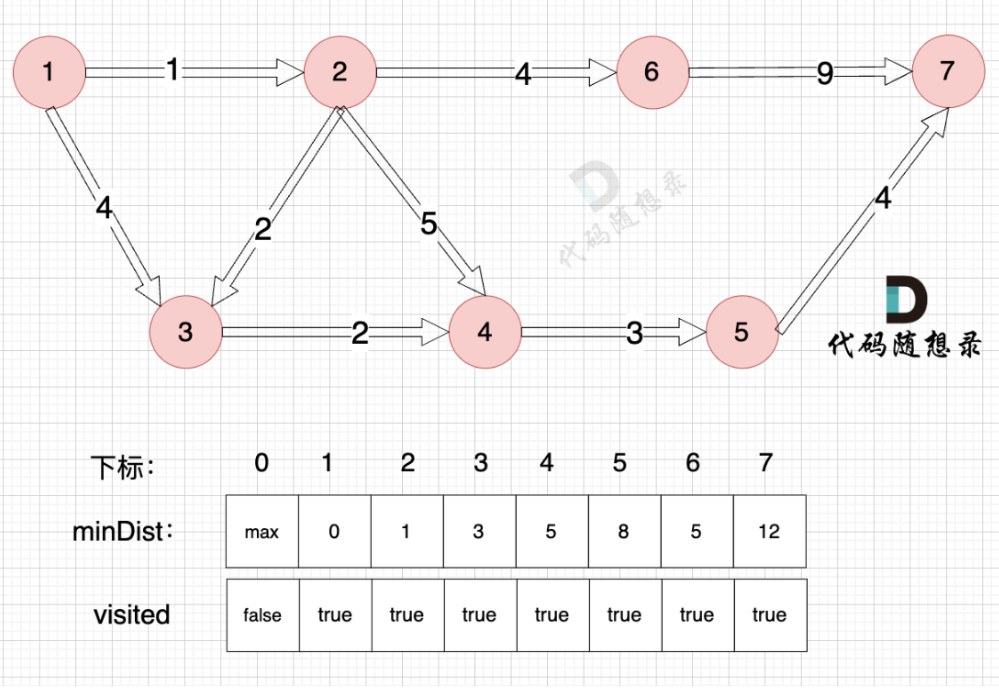
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) 
    {
        std::vector<std::vector<int>> grid(n,std::vector<int>(n,INT_MAX));
        k=k-1;
        for(auto elem:times)
        {
            elem[0]--;
            elem[1]--;
            grid[elem[0]][elem[1]]=elem[2];
        }
        std::vector<int> minDist(n,INT_MAX);
        std::vector<bool> visited(n,false);
        minDist[k]=0;

        for(int i=0;i<n;i++)
        {
            int min_index=-1;
            int min_val=INT_MAX;
            for(int i=0;i<n;i++)
            {
                if(visited[i]==false&&minDist[i]<=min_val)
                {
                    min_val=minDist[i];
                    min_index=i;
                }
            }
            visited[min_index]=true;
            for(int i=0;i<n;i++)
            {
                if(grid[min_index][i]!=INT_MAX&&visited[i]==false&&minDist[min_index]+grid[min_index][i]<minDist[i])
                {
                    minDist[i]=minDist[min_index]+grid[min_index][i];
                }
            }
        }
        int result=0;
        for(int i=0;i<n;i++)
        {
            result=std::max(result,minDist[i]);
        }
        if(result==INT_MAX) return -1;
        return result;
    }
};